Quick Summary

Using data provided by Synaptive Medical, I developed a new reconstruction algorithm for low SNR MR thermometry. It makes it possible to monitor temperatures inside the human body in real time with high spatial resolution, even at very high undersampling rates.

Real-Time Acceleration in Low SNR MR Thermometry

MR thermometry is a technique used to measure and monitor temperature changes within the body in real-time, primarily during thermal therapies such as focused ultrasound or RF ablation. This technology is crucial for ensuring that targeted tissues reach the desired temperature while avoiding damage to surrounding healthy tissues.

Real-time acceleration methods in MR thermometry are essential for providing immediate temperature feedback during these procedures. In low SNR environments, like those found in 0.5T scanners, achieving real-time imaging is challenging due to the inherently lower signal strength and higher noise levels.

Key Real-Time Acceleration Techniques:

• Parallel Imaging: Techniques like SENSE and GRAPPA enable real-time MR thermometry by utilizing multiple receiver coils to simultaneously acquire data, thereby reducing acquisition times. These methods are especially effective in low SNR environments, as they allow for rapid temperature monitoring with minimal delay, making them suitable for real-time applications.
• Echo Planar Imaging (EPI): EPI is a fast imaging technique that can acquire an entire image in a single shot, which is essential for real-time MR thermometry. Despite being prone to artifacts, EPI’s speed makes it highly valuable for continuous temperature monitoring during thermal therapies, particularly when immediate feedback is necessary.
• Model-Based Reconstruction: Integrating physical models of heat transfer directly into the reconstruction process enables the real-time estimation of temperature. This approach helps in filtering out noise and improving the accuracy of temperature maps as they are generated, ensuring that clinicians receive reliable data instantly.
• Deep Learning-Based Methods: Deep learning models, particularly those designed for real-time processing, can be employed to reconstruct temperature maps directly from incoming data streams. These models are trained to suppress noise and deliver instantaneous temperature updates, making them ideal for use in low SNR environments where fast and accurate temperature readings are critical.

Why Real-Time Acceleration is Important:

Real-time acceleration methods are vital for the precise and safe delivery of thermal therapies. By providing immediate feedback on temperature changes, these methods allow clinicians to make quick, informed decisions during the procedure, thereby enhancing treatment effectiveness and reducing the risk of damage to surrounding healthy tissues. In low-field MRI systems, where SNR is a limiting factor, real-time methods ensure that MRI-guided thermal therapies can be effectively implemented, even in settings with limited resources.

My Approach

My approach to MR thermometry is based on spatial subspaces and was developed using phantom data provided by Synaptive Medical. With this phantom data, it is known which parts of the phantom will change in temperature and the spatial distribution of these changes. A similar clinical use case might be laser ablation, where the location of temperature change is known, and the spatial distribution is generally Gaussian.

1. Constructing the Spatial Subspace: Based on the known spatial distribution and location of temperature change, I construct a high-resolution spatial subspace that can accurately represent the temperature changes.
2. Real-Time Data Acquisition and Fitting: During the ablation process, k-space data is acquired. Ideally, k-space sampling focuses on areas close to DC, where most of the information resides. As the data is acquired, I fit the spatial subspace to the incoming data in real-time.
3. Kalman Filtering for Error Correction: To account for any errors or noise in the measurement and reconstruction process, a Kalman filter is applied at each pixel (or group of pixels) independently over time, enhancing the accuracy of the temperature maps.

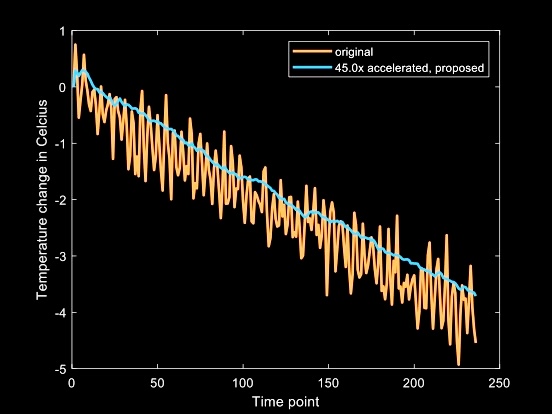
Above shows the tempoerature over time in the phantom. In orange is the original fully sampled dataset, and in blue is the result of my algorithm running on a 45x undersampled version of the same dataset. While the results with the phantom data are promising, adapting this algorithm for use with laser ablation data, where the temperature distribution is Gaussian, will require further development. This remains an area for future research.